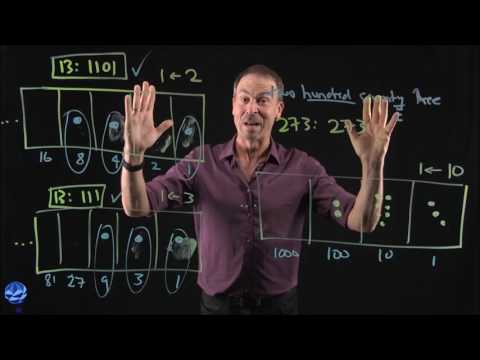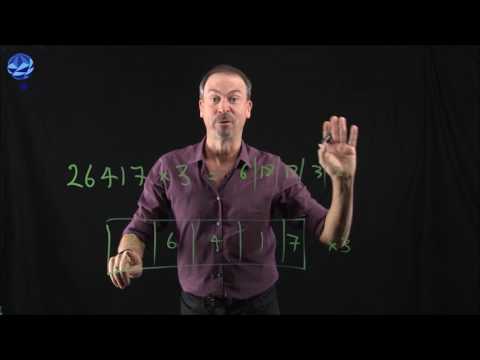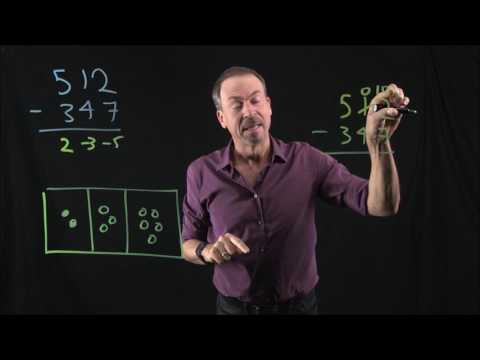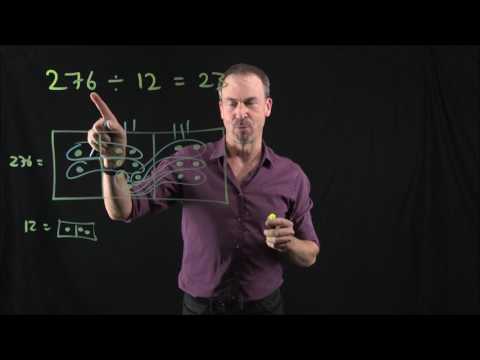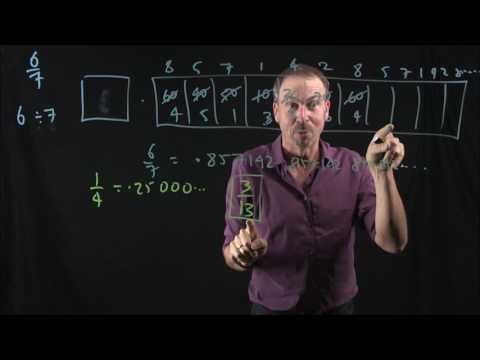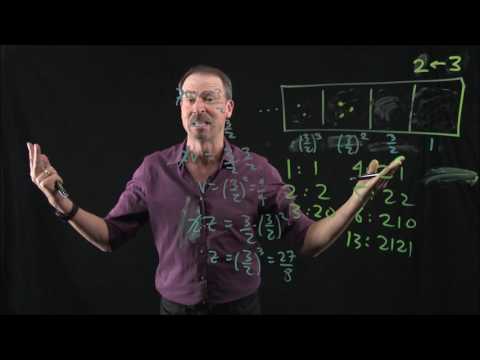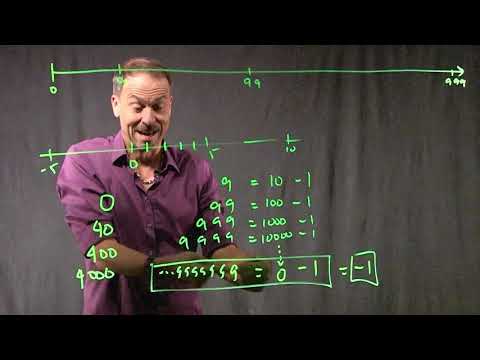The Exploding Dots experience has grown from 12 video lessons into several interactive versions.
New To Exploding Dots?
Watch the 12 video lessons which take you through the incredible journey that is Exploding Dots and download the support PDFs.
See Below!Want to Use Exploding Dots in Class?
Use the guided Desmos Classroom activities or choose DhiMath’s interactive guidebook with videos
Desmos Classroom DhiMath’s GuidebookPlay Exploding Dots Online
Just play with the DhiMath’s fully-empowered Exploding Dots widget (it does algebra!) or Mathigon’s beautiful Polypad widget
DhiMath Widget Polypad WidgetFollow our original vision of teaching Exploding Dots with the 12 experiences below. They come with multiple language versions.
Download our Guide Book and work through it with your students following the matching YouTube Playlist.
EXTRA!
See how Exploding Dots naturally sit in a high-school and university College Algebra curriculum by checking out Chapters 4, 7, and 8 of these College Algebra course notes.
Educators conduct Exploding Dots experiences with their students in any all sorts of ways — projecting videos onto a whiteboard, pausing, and having students fill in what they think James is about to do; following a lesson plan or guide assiduously and coupling it with a web-app experience; having students build dots-and-boxes models with egg cartons and beans or with students standing in big squares drawn on the floor! Create a style and approach that best suits you and your fabulous students’ style and thinking. Student “aha moments” and “mind-blown” moments are sure to be abundant. Enjoy!

EXPLORATION 1: A MYSTERIOUS MACHINE
Here we introduce and interact with a mysterious machine that sets the scene for the entire Exploding Dots story and a transformational mindset for mathematics.
Topic: Discovering place-value
Grades: All
Written guide for this Experience:
Student Handouts for this Experience:
Interactive web app for this Experience:
EXPLORATION 2: A MATHEMATICAL INSIGHT
Here we figure out what the mysterious machines are doing and discover the notion of place value. We now have a powerful visual understanding of this subtle concept that profoundly helps us understand so much grade-school, middle-school, and high-school mathematics in brand new light.
Topic: Deeply understanding place-value. Understanding why we humans are drawn to base-ten
Grades: All
Written guide for this Experience:
Student Handouts for this Experience:
Interactive web app for this Experience:
EXPLORATION 3: ADDITION AND MULTIPLICATION
Here we make profound sense of the standard algorithms.
Topic: Long Addition. Multiplication.
Grades: All, but of particular interest to K-6.
Written guide for this Experience:
Student Handouts for this Experience:
Interactive web app for this Experience:
EXPLORATION 4: SUBTRACTION
See subtraction as the addition of the opposite. This insight, coupled with the Exploding Dots machinery, provides natural and deep insight into long subtraction.
Topic: Negative numbers. Long Subtraction.
Grades: All, but of particular interest to K-6.
Written guide for this Experience:
Student Handouts for this Experience:
Interactive web app for this Experience:
EXPLORATION 5: DIVISION
Long division is made exceptionally clear.
Topic: Long Division. Long Division with remainders.
Grades: All, but of particular interest to K-6.
Written guide for this Experience:
Student Handouts for this Experience:
Interactive web app for this Experience:
EXPLORATION 6: ALL BASES, ALL AT ONCE: POLYNOMIALS
Here we discover that K-6 school arithmetic is high-school mathematics in disguise.
Topic: Polynomials. Division of Polynomials. Synthetic division in disguise.
Grades: All, but of particular interest to 7-12
Written guide for this Experience:
Student Handouts for this Experience:
Interactive web app for this Experience:
EXPLORATION 7: INFINITE SUMS
Here we play with “infinitely long polynomials,” discover the geometric series formula, and more!
Topic: The geometric series formula.
Grades: All, but of particular interest to 7-12
EXPLORATION 8: DECIMALS
Another infinite produces more boxes in the machine. We discover decimal numbers.
Topic: Decimals. Converting fractions into decimals. Constructing irrational numbers.
Grades: All, but of particular interest to 7-12
EXPLORATION 9: WEIRD AND WILD MACHINES
Now we are just playing. We discover fractional bases, negative bases, and more. Each discovery often comes with unsolved research questions.
Topic: Base-one-and-a-half and other fractional bases. Negative and other bases.
Grades: All who want to have wild intellectual fun
EXPLORATION 10: UNUSUAL NUMBERS FOR UNUSUAL MATHEMATICS
Is 0.9999…. equal to one or is it not? We explore this question and an even wilder one than that!
Topic: Convergence of infinite processes (limits). p-adic numbers.
Grades: All who want to have wild intellectual fun
EXPLORATION 11: GRAPE CODES AND NAPIER'S CHECKERBOARDS
Making Exploding Dos two dimensional allows you do conduct algebra with polynomials of two variables x and y. Scottish mathematician John Napier of the 1600s did essentially this with his multiplication checkerboard.
Topic: Napier’s historical approach to multiplication and division. Polynomial algebra with two-variables.
Grades: All who want to have wild intellectual fun
Written guide for this Experience:
Interactive web app for this Experience:
Go to this special site for this experience.
EXPLORATION 12: PUZZLES THAT CAN BE SOLVED WITH EXPLODING DOTS
Here is a collection of puzzles—some classic, some not so classic—that can be explained with Exploding Dots. Puzzles of all levels for all ages can be found here.
Topic: Puzzles galore!
Grades: Absolutely everyone.
Written guide for this Experience:
Interactive web app for this Experience:
Go to this special site for this experience.